Golden Methods to Visualize Data with Skewed Distribution
Key Techniques to Unveil Hidden Patterns in Clustered Data
Skewed data refers to data with highly uneven distribution: when the data of a variable is displayed as a histogram, the bulk of data points are either clustered on the left side of the distribution, with a long tail stretching towards the right (right-skewed), or the other way around (left-skewed), or in more complex skewed pattern. The long tail (sparse data) dominates the visual space, and squeezes the majority of the data points to the graphic corner, making it difficult to discern the underlying pattern of the clustered data majority.
In this article, I’ve summarized seven powerful strategies to visualize data with skewed distribution.
If you are R user, you can click the
show the codebutton to check the ggplot2 source code used to generate these graphs; otherwise a link to source code will be provided. If you are not an R user, you can still enjoy this article!
Use Transparency, Open Circles, Colors, and Marginal Distribution to Unveil Clustered Data Pattern
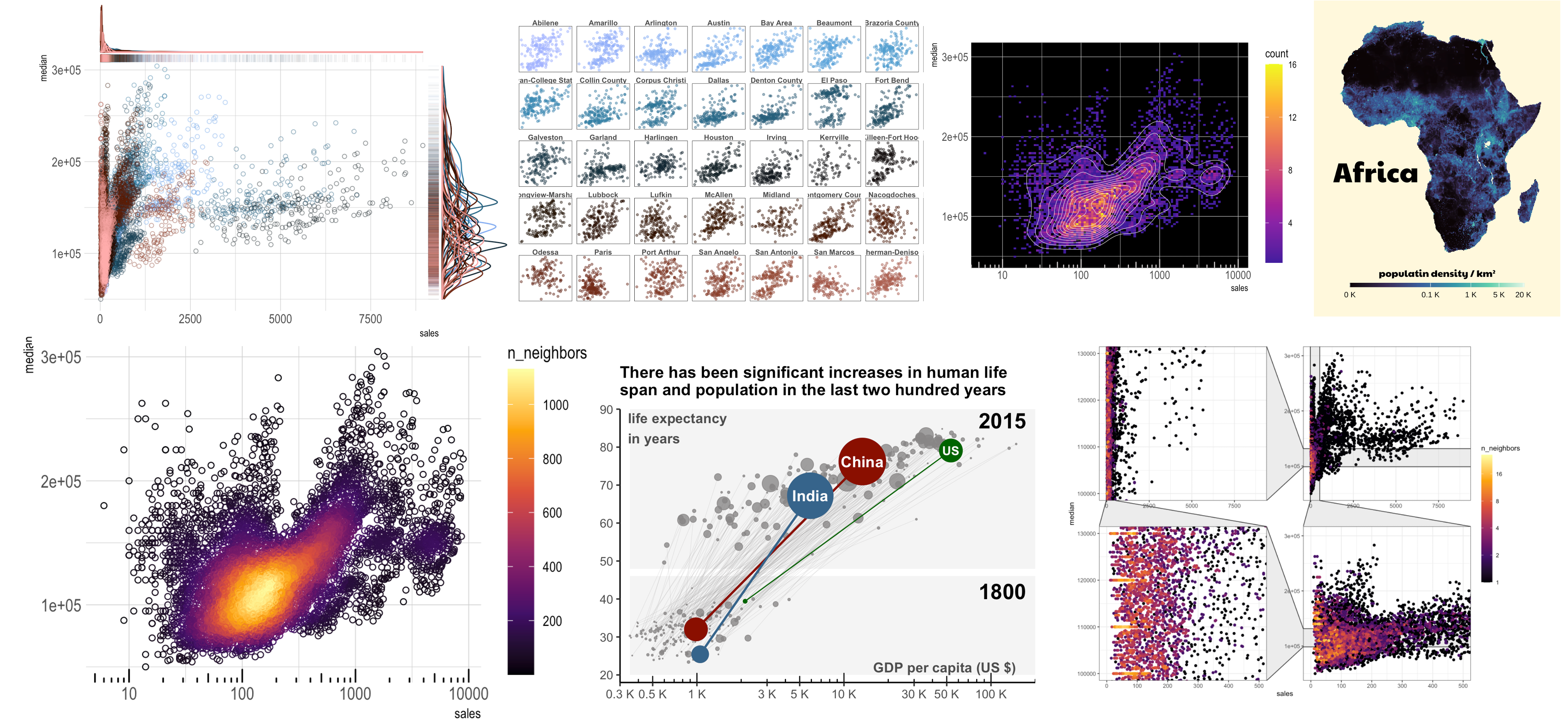
The following scatterplot displays the relationship between the housing sales and prices. The sparse data points at higher sales squeeze the majority of data to the left edge of the plot. This leads to significant data point clustering and overlap, and obscures the underlying distribution pattern.
Show the code
library(tidyverse)library(scico) # color palette
# set the default themetheme_set( hrbrthemes::theme_ipsum()+ theme( plot.title = element_text(hjust = .5, face = "bold", size = 12)))
base <- txhousing %>% ggplot(aes(x = sales, y = median))
base + geom_point(size = 1) + # discrete scale of the 'color' aesthetic ('scico' package) scale_color_scico_d(palette = "berlin") 
The following improved scatterplot employs some simple techniques to diagnose data skewness and unveil underlying data structure.
Show the code
p <- base + # map 'city' variable to 'color', with 50% transparency geom_point(aes(color = city), size = .5, alpha = .5, shape = 21) + # visualize marginal distribution as a barcode geom_rug(aes(color = city), alpha = .04, sides = "tr") + # turn off legends of both points and rugs theme(legend.position = "none") + # discrete scale of the 'color' aesthetic ('scico' package) scale_color_scico_d(palette = "berlin")
# visualize marginal distribution with the ggMarginal packageggExtra::ggMarginal(p, groupColour = T)
- Smaller point size, and shapes in outlines (such as open circles instead of solid ones) help mitigate the data overlap.
- Transparency of the data points helps unveil the amount of data clustering.
- Colors are an important tool to unveil data pattern. In this case, showing points of different cities in varied colors spotlights that the city has a profound impact on the price and sales, a significant source of data variability.
- Marginal visualization of univariate distribution shows the source of skewness. Here I displayed the distribution of sales (x axis) and prices (y axis) as barcode images and density plots. It shows that the sales is the major skewed variable.
Create Subplot Separately for Sources of Skewness
The above plot suggests that the city is an important contributing factor to the data skewness. To eliminate the effect of cities to the skewed data distribution, here we divide the plot into subplots separately for each city, with each plot having its own axis scale (labels not shown for clarity).
Show the code
base + geom_point(aes(color = city), alpha = .5, size = 1, show.legend = F) + facet_wrap(~city, scales = "free", ncol = 8) + scale_color_scico_d(palette = "berlin") + theme_void() + theme( panel.border = element_rect(color = "black", fill = NA), plot.margin = margin(rep(10, 4)), strip.text = element_text(face = "bold", color = "grey30") )
While we were lucky enough to identify the city variable as an important source of data skewness, and to reduce data skewness by creating subplots separately for each city, it’s not always easy or possible to do so in other data viz tasks. In addition, stubborn outliers can exist within a single variable, which is not solvable by creating subplots.
In the following discussion, I’ll demonstrate powerful techniques to visualize skewed dataset directly, without relying on subplots of the city variable.
Create 2D Histogram to Visualize Skewed the Data
2D histogram is one of the most efficient approaches to address data skewness encountered in a scatterplot. It creates n intervals / bins along the x and y axes, and divide the plot into a grid of n × n cells. The number of data points falling into each cell is counted, and then mapped to a color scale. Higher bin number creates a higher resolution.
Show the code
base + # Create a 2D histogram geom_bin_2d(bins = 100) + # continuous color scale of 'fill' aesthetic scale_fill_viridis_c(option = "B") + # adjust colorbar height guides(fill = guide_colorbar(barheight = unit(200, "pt"))) + theme(plot.margin = margin(rep(0, 4)))
Create 2D Density Plot
A 2D density plot is similar to the 2D histogram, but instead of creating counts in discrete intervals, it estimates the probability density function (PDF) of the underlying continuous data. (Yet the density can be drawn out in both formats, either as both continuous contours or in discrete grids.)
The density plot on the left side spotlights the extreme concentration of data points at the bottom left corner of the plot, while the rest of the sparse data points, with their minimal density values, are completely blended into background (of density of zero).
Show the code
# Create 2D density plots with density scale transformed or notf <- function( dens_exp, # raise density to power of 'dens_exp' before mapping to the color scale myTitle # plot title, noting the density transformation ){ base + stat_density_2d( # transform the density scale: # dens_exp = 1 - map the density (default) directly to color scale # dens_exp = 1/3 - map cubit root of density to color scale aes(fill = after_stat(density) ^ dens_exp), geom = "raster", # draw as grids n = 100, # at resolution of 100 bins per axis contour = F # not draw contours ) + theme(legend.position = "bottom", plot.margin = margin(0, 4)) + labs(title = myTitle, # note the density scale transformation fill = NULL) + # remove colorbar title # customize colorbar appearance guides(fill = guide_colorbar( barwidth = unit(150, "pt"), title.theme = element_text(hjust = .5))) + # continuous color scale of the 'fill' aesthetic scale_fill_viridis_c(option = "B")}
p1 <- f(dens_exp = 1, myTitle = "density (Linear)")p2 <- f(dens_exp = 1/4, myTitle = "density (cubit root)")
library(patchwork)p1 | p2 
To make those sparse data more visible, here I first converted the density values to its cubit root, which are then mapped to the color scale. Root transformation increases the value of fractional numbers (of the density values), but does not affect zeros (of the background where there is no data). This way, the transformed data points “rise” higher above the background to be easier distinguished, and nicely brings out both the concentrated data center and the sparse data regions.(This inflation effect on fractional numbers however can leads to undesired visual effect in some cases, as demonstrated in a later example.)
Scatterplot with Neighbor Number Shown in Colors
Another approach is to create a scatterplot, with each point’s local density (number of neighbors) mapped to colors. The visual effect is similar to a 2D histogram shown above, but with each individual point displayed, instead of using counting cells in a grid. Therefore, it unveils both details of individualism and overall data pattern. (In R, such visualization can be easily achieved using the geom_pointdensity() function from the ggpointdensity package.)
This approach however does not resolve the data overlap, and points buried at lower layers have low visibility, rendering the color scale less efficient. To aid in unveiling the data pattern, an effective solution is to mathematically transform the density values before mapping them to the color scale (similar to the above-mentioned 2D density plot). Here I converted each point’s neighbor number to logarithm, and then visualized the transformed values using the color scale (the colobar is labeled with original number, not the transformed result, for improved readability).
Show the code
library(ggpointdensity)
p3 <- base + # create scatterplot-density plot geom_pointdensity() + # map log2(neighbor number) to the continuous scale of 'color' aesthetic # other transformation such as 'log10' or square roots ('sqrt') also work scale_color_viridis_c(option = "B", trans = "log2", breaks = 2^(0:4)) + # increase colorbar length guides(color = guide_colorbar(barheight = unit(200, "pt"))) + ggtitle("Scatterplot with density-based colors scale")
p3
Mathematical Transform of Data Mapped to Color
You have seen from examples above how mathematical transformation effectively aids in data visualization. Yet below is my favorite example.
The heatmaps show the African population per square km: the minimum density is 0 (e.g., in most parts of Egypt on the map), and non-zero values range from 0.0000004 to 20,000; large density values are found only in limited geographic regions. The density is mirrored with the classic viridis color scale.
If without any data transformation, the map is utterly blacked out (see plot on the left): the very scattered large values (depicted in brighter colors) are overwhelmed and drowned out by the bulk of smaller numbers.

Logarithmic transformation is a common approach to deal with the widely spread data. It turns the data to a more normalized distribution, thus easier to be visualized. This approach creates a heatmap with better delineated data pattern, such as the dense population along the Nile river in Egypt. (The colorbar is labeled with original data, not the transformed data, for easier interpretation). Most parts in Egypt, however, is greyed out; as these places have population values of zero, which is not defined in logarithm, the data is treated as “missing values” (-Inf, to be specific).
Pseudo-logarithmic transformation performs the classic logarithmic operation for large numbers, but gradually transitions to a linear scale as the values approach zero. It handles large and fractional numbers and zeros (and negative numbers) in a smooth manner. Such transformation generates an impressive heatmap with well defined data pattern, highlighting the most populous geographical sites, and the dire inhospitality of the vast Saharan desert in the map. And you can find more details of the amazing technique in this article.
Compared to pseudo-log transformation, root transformation with a higher base (e.g. 7 ~ 10) yields a comparable visual effect. However, Egypt and some other places are blacked out. This is because root transformations inflate fractional numbers but leave zeros unaffected. This results in a sharp discontinuity between transformed fractional numbers and zeros, mirrored as abrupt color transition between Egypt and the surrounding areas. (You can find more discussion from the same linked-article above)

Side note: In addition to mathematical transformation of the original data, you can instead retain the original data, but strategically adjust its association with colors, and how outliers should be graphically dampened or emphasized. For instance, the following heatmaps display the incidences of infectious diseases in U.S. before and after the introduction of the vaccine (marked by the black line). The plots employ a large range of alarming yellows and reds to highlight the high incidences (the sparse data region), and only a short range of blues and greens for the bulk of low-incidence data. Such design effectively spotlighted the power of vaccination in disease control.

Mathematical Transform of Data Mirrored to Axes
Now back to the housing sale-price example. In plots below, the x-axis is transformed into a logarithmic scale of base 10. This way, the otherwise heavily clustered data points are more spread apart to unveil the data structure.
For extra fun, I’ve created out of the same data two plots yet with a different aesthetic flavor. The first one is a scatterplot, with each point’s neighbor number linearly mapped to the color scale.
Show the code
base2 <- base + # transform x-axis to log10 scale scale_x_log10() + # add log10-based ticks at the bottom side of the plot annotation_logticks(sides = "b") + guides(color = guide_colorbar(barheight = unit(200, "pt")))
# Create an open circle - density plot at a log10-transformed x-axis.base2 + geom_pointdensity(shape = 21) + scale_color_viridis_c(option = "B", breaks = seq(0, 1000, 200))
The second plot is a 2D histogram (discrete), with probability density function drawn out as contour circles (continuous).
Show the code
# A couple of technical notes:# 1. Set `begin = .1` in the color scale of the `fill` aesthetic, so that colors associated with the lowest counts start from brighter colors, not black, to be distinguished from the background.# 2. Ticks color should be set within `annotation_logticks()`; setting in `axis.ticks` in `theme()` is not effective.
base2 + geom_bin_2d(bins = 100) + scale_fill_viridis_c(option = "C", begin = .1) + guides(fill = guide_colorbar(barheight = unit(200, "pt"))) + theme(panel.background = element_rect(fill = "black")) + annotation_logticks(sides = "b", colour = "snow3") + # sketch out the contour circles geom_density2d(color = "snow2", linewidth = .2)
As another example, the scatterplot below shows the increase of GDP and human life expectancy from 1800s to 2015. It illustrates the use of axial logarithmic transformation to unfold otherwise clustered dataset. Note that while the x-axis is on log10 scale, the labels are annotated with original data values.

Note that not all mathematical transformations change the distribution profile. For instance, the commonly used standardization into z-scores (centering by mean and scaling by standard deviation) or normalization into the range [0, 1] (shifting by the minimum and scaling by the range between the max and min) do NOT change the distribution profile in this context. These methods are NOT effective in visualizing skewed data (though they are important in multivariate modeling and related visualizations such as principle component analysis).
Zoom-in Over the Clustered Data Region
It’s a good idea to zoom in over clustered regions of interest for better visual display. (In R, this can be easily realized using the facet_zoom() function from the ggforce package.)
Show the code
library(ggforce)
p3 + # reset theme to black-white theme_bw() + # zoom in over specified axial ranges facet_zoom( xlim = c(0, 500), ylim = c(1 * 10^5, 1.3 * 10^5), split = T, # show separate zoom-in over x an y, and both axes zoom.size = 1) # same size as the main plot 


